Jellium and jellium slabs

In this tutorial, we will compute the ground state of a uniform electron gas, as well as the one of a jellium slab, which is a good model for metallic surfaces.

Jellium

Let us start by performing a calculation for a uniform electrom gas, or jellium. In this tutorial, we choose as an example a Wigner-Seitz radius $r_s=5.0$. We then create a cubic box with the number of electron corresponding to the density $n$ given by

$$ \frac{1}{n} = \frac{4}{3}\pi r_s^3 $$

For doing so, we define a constant potential in the box using the Species block, as done in the input file below

CalculationMode = gs
FromScratch = yes
PeriodicDimensions = 3
BoxShape = parallelepiped

ExperimentalFeatures = yes

aCell = 1.6*angstrom
%LatticeParameters
 aCell | aCell | aCell
 90 | 90 | 90
%

r_s = 5.0 
dens = 1/(4/3*pi*r_s^3)
N_electrons = aCell^3 * dens

%Species
"jellium" | species_user_defined | potential_formula | "dens" | valence | N_electrons
%

%Coordinates
"jellium" | 0 | 0 | 0
%

Spacing = 0.7

Smearing = 0.01*eV
SmearingFunction = fermi_dirac

ExtraStates = 8
Eigensolver = chebyshev_filter

%KPointsGrid
 8 | 8 | 8
%
KPointsUseSymmetries = yes

Jellium slab

In order to describe a jellium slab, we need to use the special Species call “species_jellium_slab”. This species has two relevant parameters, one is the thickness of the slab, and one is the number of electrons. This is specified as follow:

%Species
"jellium" | species_jellium_slab | thickness | d0 | valence | N_electrons
%

where “d_0” and “N_electrons” are values defined in the input file. As the homogeneous electrons gas are usually parametrized by the Wigner-Seitz radius $r_s$, the number of electrons in the slab can be defined as

$$ N_e = A d_0 / (4 \pi r_s^3 / 3) $$

where $A$ is the area of the slab included in the simulation box.

The full input file then reads

CalculationMode = gs
FromScratch = yes
PeriodicDimensions = 2
BoxShape = parallelepiped

ExperimentalFeatures = yes

aCell = 1.6*angstrom
%LatticeParameters
 aCell | aCell | 25*angstrom
 90 | 90 | 90
%

r_s = 5.0 
d0 = 16.0*angstrom
N_electrons = aCell^2 * d0 / (4/3*pi*r_s^3)  

%Species
"jellium" | species_jellium_slab | thickness | d0 | valence | N_electrons
%

%Coordinates
"jellium" | 0 | 0 | 0
%

Spacing = 0.7

Smearing = 0.01*eV
SmearingFunction = fermi_dirac

ExtraStates = 4
Eigensolver = chebyshev_filter

%KPointsGrid
 12 | 12 | 1
%
KPointsUseSymmetries = yes

%Output
 density | axis_z
%

Here, we used a unit cell of $1.6\text{\AA}\times1.6\text{\AA}$ in-plane size, and a size along the perpendicular direction of $25 \text{\AA} $. We then a jellium slab of thickness $16 \text{\AA} $, centered here around $z=0$, with $r_s=5$, which correspond to 0.5279 electrons in the system. Because of the fractional occupations, and because we describe a metallic surface, we employed here a small Smearing of 10 meV, with a Fermi-Dirac distribution.

After running this input file, one can plot the density of the jellium slab.

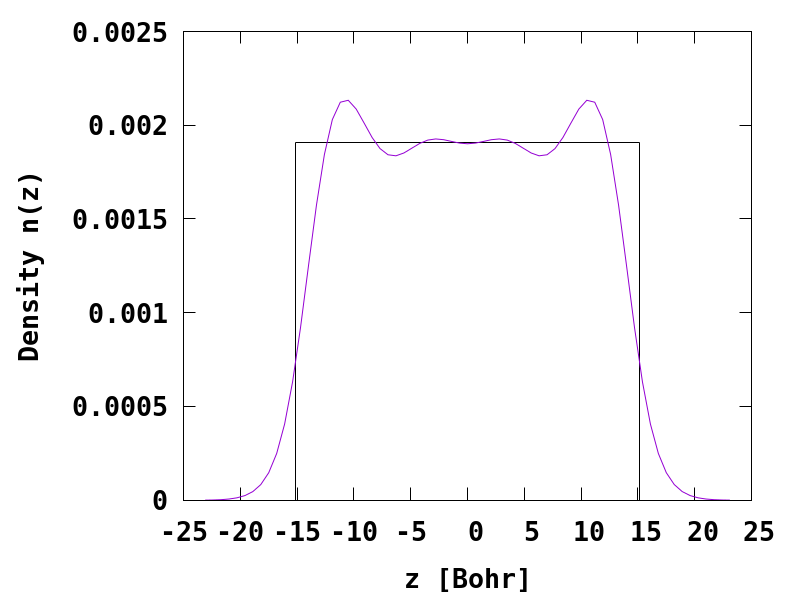
Clear Friedel oscillations of the electron density near the surface are observed, and the result can be compared to the result obtained by Lang and Kohn, see Fig. 2 in Ref.¹.

This plot is generated from the script:

set xlabel "z [Bohr]"
set ylabel "Density n(z)"
set t pngcairo font "Monospace-Bold,20" size 800, 600

set output "jellium_slab_density.png"

rs = 5.0
rho = 1/(4.0/3.0*pi*(rs**3))
Lz = 30.2356/2

set arrow nohead from -Lz,0 to -Lz,rho
set arrow nohead from Lz,0 to Lz,rho
set arrow nohead from -Lz,rho to Lz,rho

plot 'static/density.x=0,y=0' w l notitle

References