DFT+U+V
This tutorial aims at explaining how to perform DFT+U+V calculations in Octopus. This correspond to adding not only an on-site Hubbard interaction U, but also an intersite interaction V. As a prototypical example, we will consider bulk silicon.
The DFT+U+V method, as well as its performances and implementation details are discussed in Ref.1
Input
The input file we will use is the following one:
CalculationMode = gs
PeriodicDimensions = 3
Spacing = 0.5
%LatticeVectors
0.0 | 0.5 | 0.5
0.5 | 0.0 | 0.5
0.5 | 0.5 | 0.0
%
a = 10.18
%LatticeParameters
a | a | a
%
%ReducedCoordinates
"Si" | 0.0 | 0.0 | 0.0
"Si" | 1/4 | 1/4 | 1/4
%
nk = 2
%KPointsGrid
nk | nk | nk
0.5 | 0.5 | 0.5
0.5 | 0.0 | 0.0
0.0 | 0.5 | 0.0
0.0 | 0.0 | 0.5
%
ExtraStates = 4
%KPointsPath
10 | 10 | 15
0.5 | 0.0 | 0.0 # L point
0.0 | 0.0 | 0.0 # Gamma point
0.0 | 0.5 | 0.5 # X point
1.0 | 1.0 | 1.0 # Another Gamma point
%
DFTULevel = dft_u_acbn0
AOLoewdin = yes
UseAllAtomicOrbitals = yes
SkipSOrbitals = no
ACBN0IntersiteInteraction = yes
ACBN0IntersiteCutoff = 7
ExperimentalFeatures = yes
Most of the variable are the same as in the introduction tutorial on solids [Getting started with periodic systems](../Getting started with periodic systems), and the DFT+U related variables are explained in the tutorial DFT+U. For convenience, we are doing here a ground-state calculation with a k-point grid and a k-point path. This allows to get the bandstructure as a direct output of a ground-state calculation. However, the unoccupied states might not be converged with this approach. To perform a proper band-structure calculation, see the tutorial [Getting started with periodic systems](../Getting started with periodic systems).
Compared to a more conventional DFT+U calculation, we note few differences here:
- AOLoewdin
= yes: We want to perform a Löwdin orthonormalization of the atomic orbitals. This is very important to avoid double counting between different orbitals. - UseAllAtomicOrbitals
= yesand SkipSOrbitals= no: Here we want to use all the atomic orbitals available in the pseudopotentials. In this case, the s orbitals are important to obtain a meaningful orthonormalization. Note that in Si, we indeed want to use all atomic orbitals. But in some strongly correlated materials, one might as well only use one set of atomic orbital using the Species block, as done for NiO in the DFT+U tutorial. - ACBN0IntersiteInteraction
= yes: We are asking for the intersite interaction (+V). The number of neighbors for which we are including the intersite interaction is given by a cutoff in real space, specified by the variable ACBN0IntersiteCutoff. Here we are using 7 Bohr, which gives us the first nearest neighbor only. In practice, this value needs to be converged, or needs to be chosen if one wants to include only certain shells of neighbors.
Output
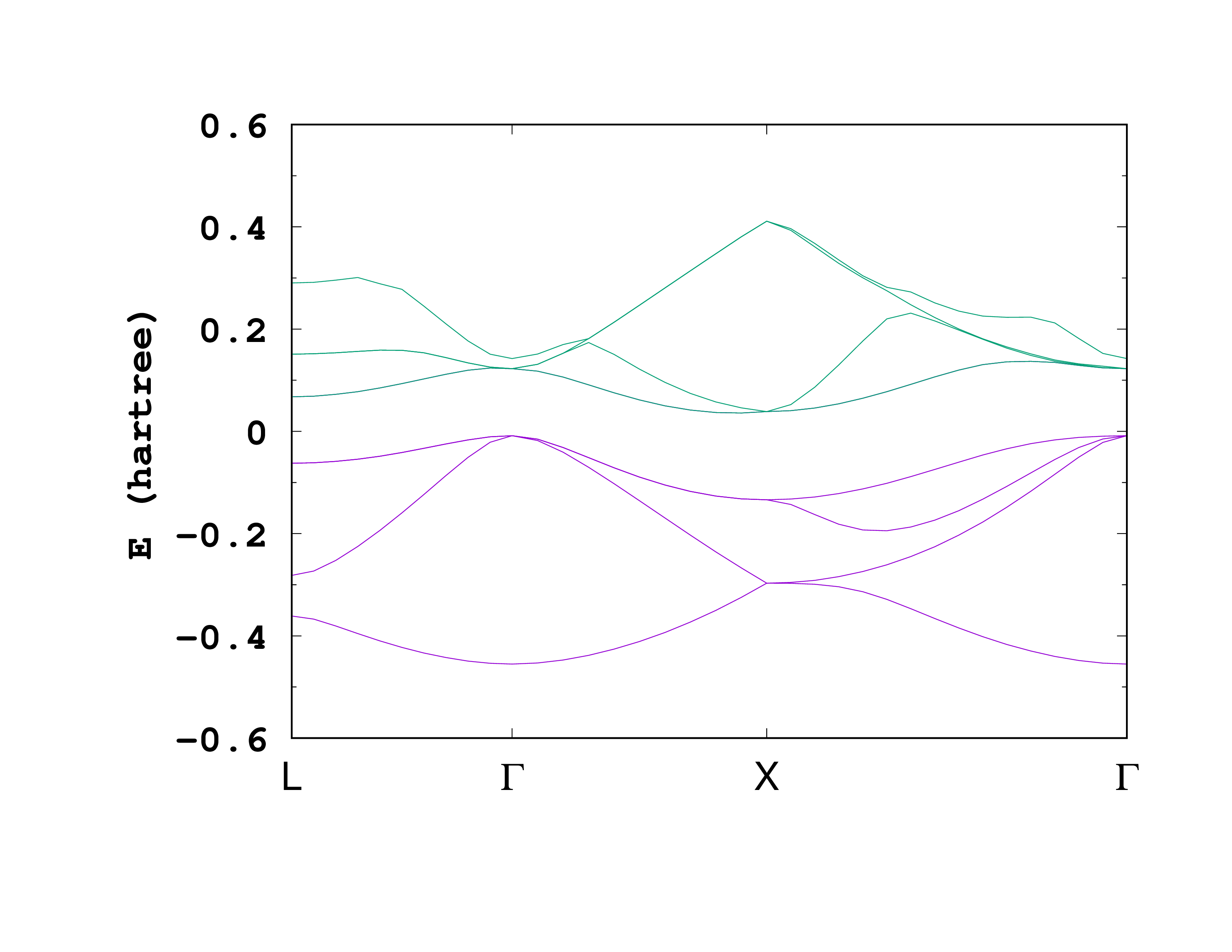
After running Octopus using the above input, we can look at the output. In the static/info file, we find the direct and indirect bandgap
Direct gap at ik= 2 of 0.0304 H
Indirect gap between ik= 8 and ik= 2 of 0.0177 H
Direct gap at ik= 6 of 0.1346 H
Indirect gap between ik= 6 and ik= 24 of 0.1148 H
As a comparison, without adding the +U+V, one finds at the LDA level a much smaller bandgap
Direct gap at ik= 14 of 0.1346 H
Indirect gap between ik= 2 and ik= 11 of 0.1148 H
Direct gap at ik= 1 of 0.1041 H
Indirect gap between ik= 3 and ik= 9 of 0.0810 H
The effect of bandgap opening can be understood more precisely from the bandstructure. As one can see, the conduction bands have been rigidly shifted toward higher energies, as expected from more advance calculations such as hybrid functionals or GW calculations.
References
-
N. Tancogne-Dejean, and A. Rubio, Parameter-free hybridlike functional based on an extended Hubbard model: DFT+U+V, Physical Review B 102 155117 (2020); ↩︎