Triplet excitations
In this tutorial, we will calculate triplet excitations for methane with time-propagation and Casida methods.
Time-propagation
Ground-state
We begin with a spin-polarized calculation of the ground-state, as before but with SpinComponents = spin_polarized specified now.
CalculationMode = gs
UnitsOutput = eV_angstrom
Radius = 6.5*angstrom
Spacing = 0.24*angstrom
CH = 1.097*angstrom
%Coordinates
"C" | 0 | 0 | 0
"H" | CH/sqrt(3) | CH/sqrt(3) | CH/sqrt(3)
"H" | -CH/sqrt(3) |-CH/sqrt(3) | CH/sqrt(3)
"H" | CH/sqrt(3) |-CH/sqrt(3) | -CH/sqrt(3)
"H" | -CH/sqrt(3) | CH/sqrt(3) | -CH/sqrt(3)
%
SpinComponents = spin_polarized
You can verify that the results are identical in detail to the non-spin-polarized calculation since this is a non-magnetic system.
Time-propagation
Next, we perform the time-propagation using the following input file:
CalculationMode = td
UnitsOutput = eV_angstrom
Radius = 6.5*angstrom
Spacing = 0.24*angstrom
CH = 1.097*angstrom
%Coordinates
"C" | 0 | 0 | 0
"H" | CH/sqrt(3) | CH/sqrt(3) | CH/sqrt(3)
"H" | -CH/sqrt(3) |-CH/sqrt(3) | CH/sqrt(3)
"H" | CH/sqrt(3) |-CH/sqrt(3) | -CH/sqrt(3)
"H" | -CH/sqrt(3) | CH/sqrt(3) | -CH/sqrt(3)
%
SpinComponents = spin_polarized
TDPropagator = aetrs
TDTimeStep = 0.004/eV
TDMaxSteps = 2500 # ~ 10.0/TDTimeStep
TDDeltaStrength = 0.01/angstrom
TDPolarizationDirection = 1
TDDeltaStrengthMode = kick_spin
Besides the SpinComponents variable, the main difference is the type of perturbation that is applied to the system. By setting
TDDeltaStrengthMode = kick_spin, the kick will have opposite sign for up and down states. Whereas the ordinary kick (kick_density) yields the response to a homogeneous electric field, i.e. the electric dipole response, this kick yields the response to a homogeneous magnetic field, i.e. the magnetic dipole response. Note however that only the spin degree of freedom is coupling to the field; a different calculation would be required to obtain the orbital part of the response. Only singlet excited states contribute to the spectrum with kick_density, and only triplet excited states contribute with kick_spin. We will see below how to use symmetry to obtain both at once with kick_spin_and_density.
Spectrum
When the propagation completes, run the oct-propagation_spectrum utility to obtain the spectrum. This is how the cross_section_vector should look like.
# nspin 2
# kick mode 1
# kick strength 0.005291772086
# dim 3
# pol(1) 1.000000000000 0.000000000000 0.000000000000
# pol(2) 0.000000000000 1.000000000000 0.000000000000
# pol(3) 0.000000000000 0.000000000000 1.000000000000
# direction 1
# Equiv. axes 0
# wprime 0.000000000000 0.000000000000 1.000000000000
# kick time 0.000000000000
#%
# Number of time steps = 2500
# PropagationSpectrumDampMode = 2
# PropagationSpectrumDampFactor = -27.2114
# PropagationSpectrumStartTime = 0.0000
# PropagationSpectrumEndTime = 10.0000
# PropagationSpectrumMinEnergy = 0.0000
# PropagationSpectrumMaxEnergy = 20.0000
# PropagationSpectrumEnergyStep = 0.0100
#%
# Energy sigma(1, nspin=1) sigma(2, nspin=1) sigma(3, nspin=1) sigma(1, nspin=2) sigma(2, nspin=2) sigma(3, nspin=2) StrengthFunction(1) StrengthFunction(2)
# [eV] [A^2] [A^2] [A^2] [A^2] [A^2] [A^2] [1/eV] [1/eV]
0.00000000E+00 -0.00000000E+00 -0.00000000E+00 -0.00000000E+00 -0.00000000E+00 -0.00000000E+00 -0.00000000E+00 -0.00000000E+00 -0.00000000E+00
0.10000000E-01 -0.41162108E-08 -0.27945647E-16 0.45982882E-16 0.40117139E-08 0.64453830E-16 0.31116227E-16 -0.37501587E-08 0.36549547E-08
0.20000000E-01 -0.16407193E-07 -0.11165153E-15 0.18372002E-15 0.15989541E-07 0.25750965E-15 0.12430761E-15 -0.14948112E-07 0.14567601E-07
0.30000000E-01 -0.36700806E-07 -0.25072524E-15 0.41257814E-15 0.35762345E-07 0.57825221E-15 0.27910319E-15 -0.33437026E-07 0.32582022E-07
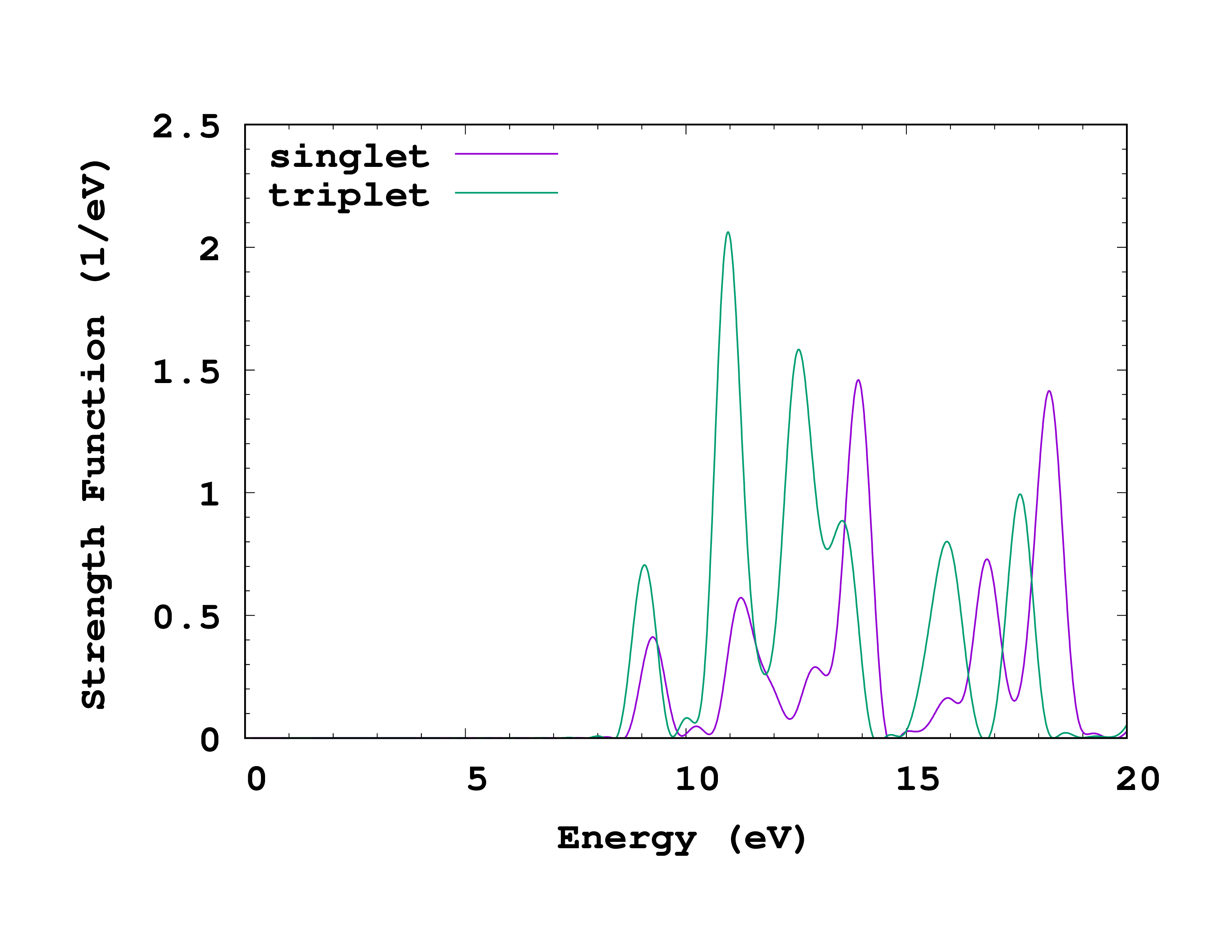
You can see that there are now separate columns for cross-section and strength function for each spin. The physically meaningful strength function for the magnetic excitation is given by StrengthFunction(1) - StrengthFunction(2) (since the kick was opposite for the two spins). (If we had obtained cross_section_tensor
, then the trace in the second column would be the appropriate cross-section to consider.) We can plot and compare to the singlet results obtained before. You can see how this looks on the right. The first triplet transition is found at 9.05 eV, slightly lower energy than the lowest singlet transition.
If you are interested, you can also repeat the calculation for TDDeltaStrengthMode = kick_density (the default) and confirm that the result is the same as for the non-spin-polarized calculation.
Using symmetries of non-magnetic systems
As said before, methane is a non-magnetic system, that is, the up and down densities are the same and the magnetization density is zero everywhere:
$$ \rho^{\uparrow}(\mathbf r) = \rho^{\downarrow}(\mathbf r) $$
Note that it is not enough that the total magnetic moment of the system is zero as the previous condition does not hold for anti-ferromagnetic systems. The symmetry in the spin-densities can actually be exploited in order to obtain both the singlet and triplet spectra with a single calculation. This is done by using a special perturbation that is only applied to the spin up states.1
To use this perturbation, we need to set TDDeltaStrengthMode = kick_spin_and_density. If you repeat the time-propagation with this kick, you should obtain a different cross_section_vector
file containing both the singlet and triplet spectra. The singlets are given by StrengthFunction(1) + StrengthFunction(2), while the triplets are given by StrengthFunction(1) - StrengthFunction(2).
Casida equation
The calculation of triplets with the casida mode for spin-polarized systems is currently not implement in Octopus. Nevertheless, just like for the time-propagation, we can take advantage that for non-magnetic systems the two spin are equivalent. In this case it allow us to calculate triplets without the need for a spin-polarized run. The effective kernels in these cases are:
$f_{\rm Hxc}^{\rm singlet} \left[ \rho \right] = f^{\uparrow}_{\rm Hxc} \left[ \rho ^{\uparrow} \right] + f^{\uparrow}_{\rm Hxc} \left[ \rho^{\downarrow} \right] = f_{\rm H} \left[ \rho \right] + f^{\uparrow}_{\rm xc} \left[ \rho ^{\uparrow} \right] + f^{\uparrow}_{\rm xc} \left[ \rho^{\downarrow} \right]$
$f_{\rm Hxc}^{\rm triplet} \left[ \rho \right] = f^{\uparrow}_{\rm Hxc} \left[ \rho ^{\uparrow} \right] - f^{\uparrow}_{\rm Hxc} \left[ \rho^{\downarrow} \right] = f^{\uparrow}_{\rm xc} \left[ \rho ^{\uparrow} \right] - f^{\uparrow}_{\rm xc} \left[ \rho^{\downarrow} \right]$
Therefore, we start by doing a ground-state and unoccupied states runs exactly as was done in the Optical spectra from Casida tutorial. Then, do a Casida run with the following input file:
CalculationMode = casida
UnitsOutput = eV_angstrom
Radius = 6.5*angstrom
Spacing = 0.24*angstrom
CH = 1.097*angstrom
%Coordinates
"C" | 0 | 0 | 0
"H" | CH/sqrt(3) | CH/sqrt(3) | CH/sqrt(3)
"H" | -CH/sqrt(3) |-CH/sqrt(3) | CH/sqrt(3)
"H" | CH/sqrt(3) |-CH/sqrt(3) | -CH/sqrt(3)
"H" | -CH/sqrt(3) | CH/sqrt(3) | -CH/sqrt(3)
%
ExtraStates = 10
CasidaCalcTriplet = yes
ExperimentalFeatures = yes
The only difference with respect to the calculation of the singlets, is the CasidaCalcTriplet input variable.
Once the Casida calculation is finished, run oct-casida_spectrum , plot the results, and compare to the singlet calculation. Below you can see how this plot should look like.
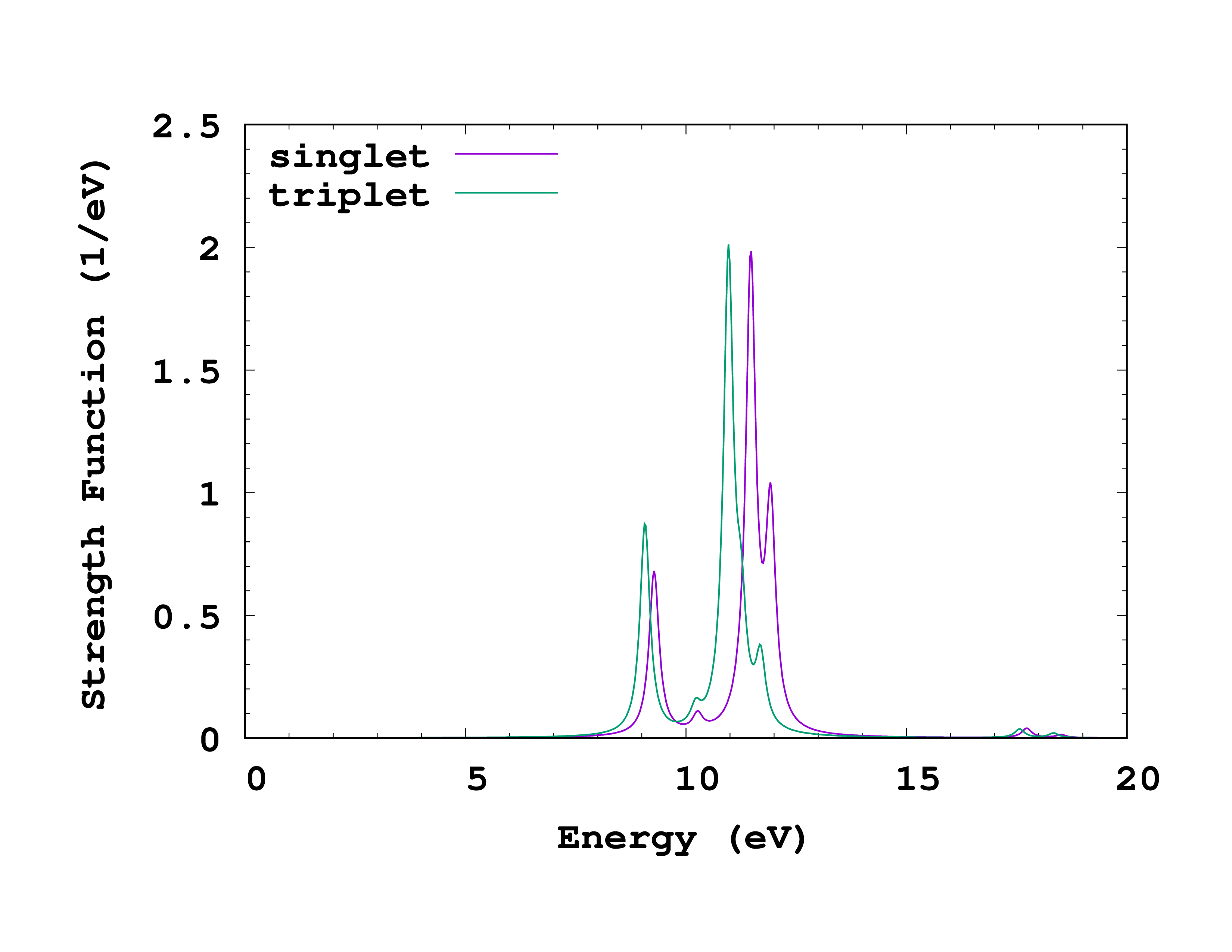
How do the singlet and triplet energy levels compare? Can you explain a general relation between them? How does the run-time compare between singlet and triplet, and why?
Comparison
As for the singlet spectrum, we can compare the time-propagation and Casida results. What is the main difference, and what is the reason for it?
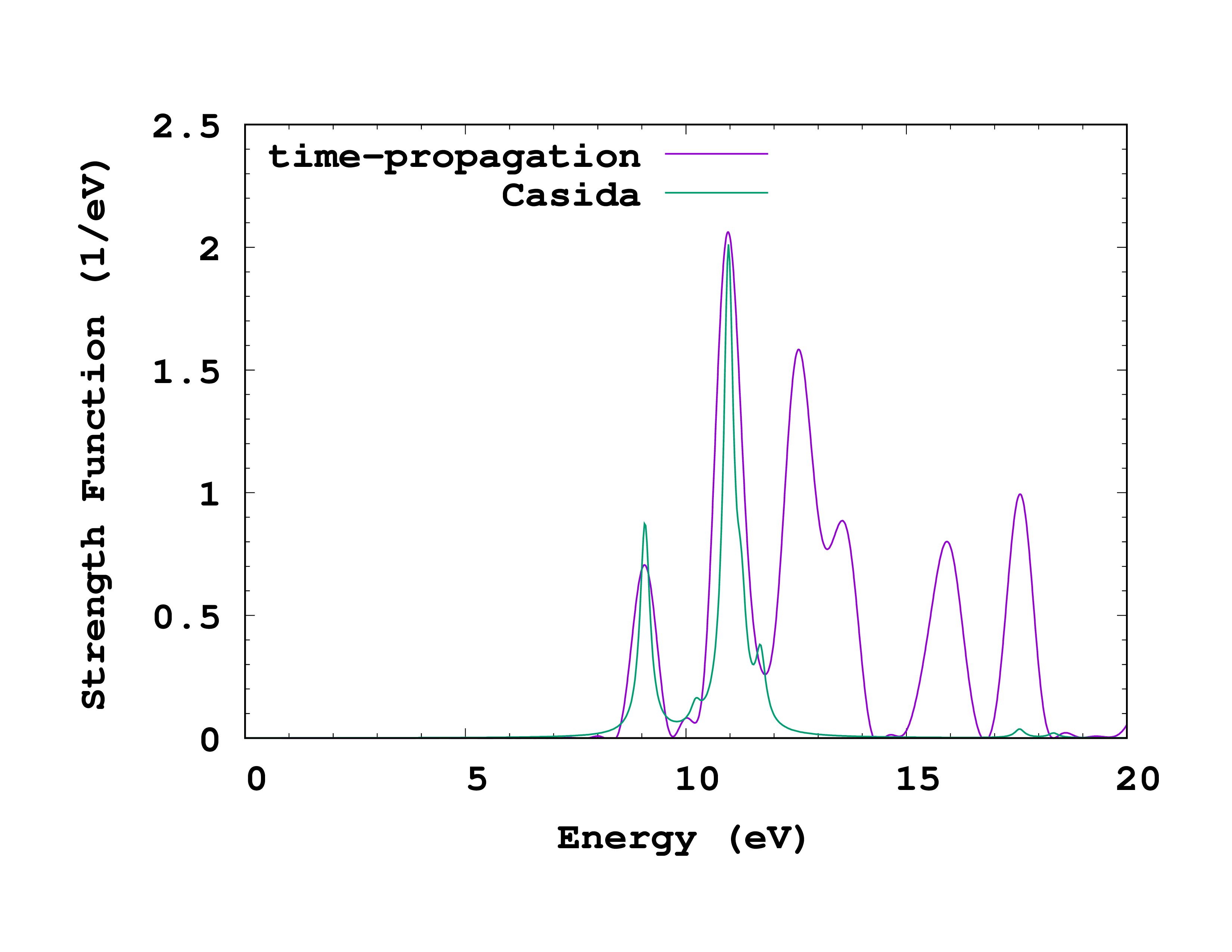
-
M.J.T. Oliveira, A. Castro, M.A.L. Marques, and A. Rubio, On the use of Neumann's principle for the calculation of the polarizability tensor of nanostructures, J. Nanoscience and Nanotechnology 8 1-7 (2008); ↩︎