☰
Navigation :

Dispersive linear media

In addition to the possibility to include objects described as static linear media, Octopus allows for simulations with dispersive media. For example, let’s consider the following input file, for propagation of a pulse through a sphere described by a Drude polarizability:


CalculationMode = td
ExperimentalFeatures = yes
Restartwalltimeperiod = 1.1
%Systems
 'Maxwell' | maxwell
 'NP' | dispersive_medium
%

 MediumPoleEnergy = 9.03*ev
 MediumPoleDamping = 0.053*ev
 MediumDispersionType = drude_medium
 %MediumCurrentCoordinates
   -160.0*nm | 0.0 | 0.0
   -80.0*nm | 0.0 | 0.0
%
# ----- Maxwell box variables ---------------------------------------------------------------------

 l_zero = 550*nm     #central wavelength
 lsize_mx = 1.25*l_zero
 lsize_myz = 0.5*l_zero
 S_c = 0.2 ##Courant condition coefficient

 dx_mx    = 20*nm
 BoxShape   = parallelepiped
 NP.BoxShape = box_cgal
 NP.BoxCgalFile = "gold-np-r80nm.off"

%Lsize
 lsize_mx+0.25*l_zero | lsize_myz+0.25*l_zero | lsize_myz+0.25*l_zero
%

%Spacing
 dx_mx | dx_mx | dx_mx
%

%MaxwellBoundaryConditions
 plane_waves | zero | zero
%

%MaxwellAbsorbingBoundaries
 cpml | cpml | cpml
%

MaxwellABWidth              = 0.25*l_zero
MaxwellABPMLPower           = 3.0
MaxwellABPMLReflectionError = 1e-16

OutputFormat = axis_x + plane_y

%MaxwellOutput
 electric_field
 total_current_mxll
%

MaxwellOutputInterval = 20
MaxwellTDOutput       = maxwell_energy + maxwell_total_e_field

%MaxwellFieldsCoordinate
  -120.0*nm | 0.0 | 0.0
  -80.0*nm | 0.0 | 0.0
  -20.0*nm | 0.0 | 0.0
%

Maxwell.TDSystemPropagator = prop_expmid
NP.TDSystemPropagator      = prop_rk4

timestep                = S_c*dx_mx/c
TDTimeStep              = timestep
TDPropagationTime       = 240*timestep

lambda = l_zero
omega  = 2 * pi * c / lambda
kx     = omega / c
Ez    = 1.0
sigma = 40.0*c
p_s     = -lsize_mx*1.2

%UserDefinedInitialMaxwellStates
 use_incident_waves
%

%MaxwellIncidentWaves
 plane_wave_mx_function | 0 | 0 | Ez | "plane_waves_function"
%

%MaxwellFunctions
 "plane_waves_function" | mxf_gaussian_wave | kx | 0 | 0 | p_s | 0 | 0 | sigma
%

Here, we need to define the variables MediumPoleEnergy and MediumPoleDamping, which represent the plasma frequency $\omega_p$ and inverse lifetime $\gamma$ of a Drude pole. For this example, the parameters are those for the Drude peak of gold, as taken from the literature 1. Also, we can define MediumCurrentCoordinates to obtain the polarization current at certain points. The rest of the input variables of the medium are the same that have been used for the static linear medium. In this case, we are using an off file that contains the shape of a sphere of 80 nm radius, which is displaced from the origin by one radius to the negative x direction.

off file

For practical reasons, we set the box size as a function of the incoming pulse wavelength l_zero, and we make the box larger in the direction of propagation. We also add the spacing needed for the PML boundaries, defined below. As you can see, this is defined as 550 nm, using the default parameter nm to convert it to atomic units. Also, we set a relatively small Courant number, which will replace the $1/\sqrt(3)$ value that was explained before. This is because for Drude media, the time step is also limited by the plasma frequency of the metal, and not only by the grid spacing, so a larger value will cause the simulation to explode (you are welcome to try and increase it, plot the total integrated energy, and observe the divergence after the threshold). For this setup, 0.1 is an appropriate Courant number.

After we run the simulation, we can plot again the z-component of the electric field in the xz-plane for three different time steps, using the following script:

gnuplot script

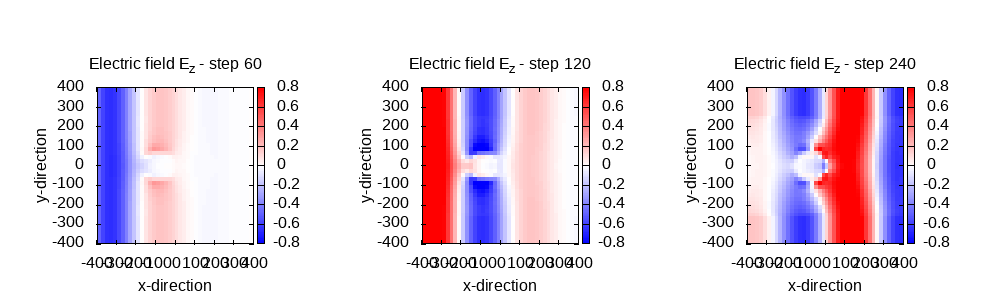
The plot we get is the following:

As it is expected, as the medium reacts to the external field via its polarization current density, screening it inside the sphere, as it is expected from a metal. We can also note that the space discretization used is a rather coarse mesh in this tutorial, due to computation time, but the outcomes are still reasonable.

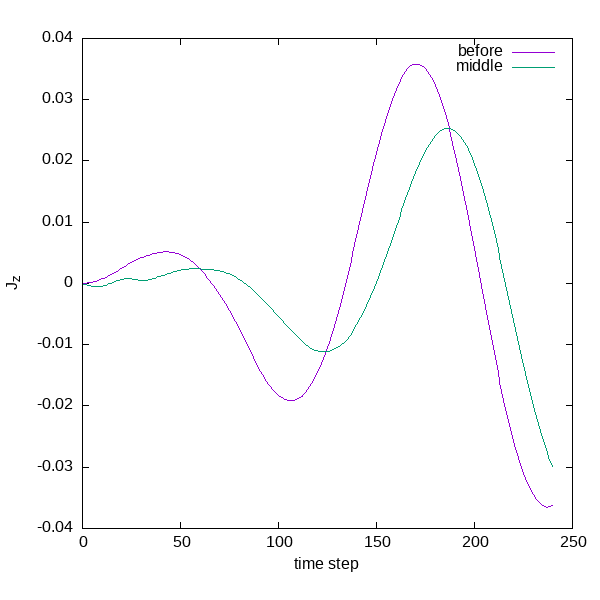
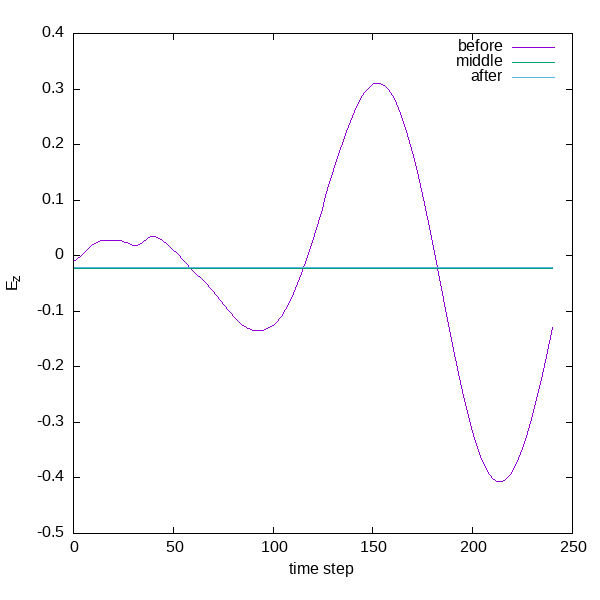
Finally, we can examine how these currents arise in time. Using the following script we can plot the current at three different points (the ones we requested in the input file, namely: near the surface of the sphere towards the negative x axis, in the middle, and near the surface on the positive x axis). Also we plot the E field at these points.

gnuplot script

As can be seen, the current in the direction of the incident electric field (called “before”) is larger, screening the field effectively. This can be seen by plotting the electric field in the other points, where the values in the “middle” and “after” are much smaller than “before” (actually, the plotted field has already been quenched by the medium, otherwise the waveform would be that of the Gaussian envelope used). In addition to scattering, there is absorption of energy by the nanoparticle, given by the imaginary part of the polarizability. Using a setup like this, and processing the proper values of the EM field in full space and time, it would be possible to calculate an extinction spectrum of the sphere, which can be compared to the one calculated using Mie theory, or other methods.

  1. Aleksandar D. Rakić, Aleksandra B. Djurišić, Jovan M. Elazar, and Marian L. Majewski, Optical properties of metallic films for vertical-cavity optoelectronic devices, Applied Optics 37 5271 (1998); ↩︎