1D Helium
The next example will be the helium atom in one dimension which also has two electrons, just as we used for the harmonic oscillator. The main difference is that instead of describing two electrons in one dimension we will describe one electron in two dimensions. The calculation in this case is not a DFT one, but an exact solution of the Schrödinger equation – not an exact solution of the helium atom, however, since it is a one-dimensional model.
Equivalence between two 1D electrons and one 2D electron
To show that we can treat two electrons in one dimension as one electron in two dimensions, lets start by calling $x,$ and $y,$ the coordinates of the two electrons. The Hamiltonian would be (note that the usual Coulomb interaction between particles is usually substituted, in 1D models, by the soft Coulomb potential, $u(x)=(1+x^2)^{(-1/2)}\,$):
$$ \hat{H} = -\frac{1}{2}\frac{\partial^2}{\partial x^2} -\frac{1}{2}\frac{\partial^2}{\partial y^2} +\frac{-2}{\sqrt{1+x^2}}+\frac{-2}{\sqrt{1+y^2}}+\frac{1}{\sqrt{1+(x-y)^2}}. $$
Instead of describing two electrons in one dimension, however, we may very well think of one electron in two dimensions, subject to a external potential with precisely the shape given by:
$$ \frac{-2}{\sqrt{1+x^2}}+\frac{-2}{\sqrt{1+y^2}}+\frac{1}{\sqrt{1+(x-y)^2}} \,, $$
Since the Hamiltonian is identical, we will get the same result. Whether we regard $x,$ and $y,$ as the coordinates of two different particles in one dimension or as the coordinates of the same particle along the two axes in two dimensions is entirely up to us. (This idea can actually be generalized to treat two 2D particles via a 4D simulation in Octopus too!) Since it is usually easier to treat only one particle, we will solve the one-dimensional helium atom in two dimensions. We will also therefore get a “two-dimensional wave-function”. In order to plot this wave-function we specify an output plane instead of an axis.
Input
With the different potential and one more dimension the new input file looks like the following
CalculationMode = gs
Dimensions = 2
TheoryLevel = independent_particles
BoxShape = parallelepiped
Lsize = 8
Spacing = 0.1
%Output
wfs | plane_z
%
%Species
"helium" | species_user_defined | potential_formula | "-2/(1+x^2)^(1/2)-2/(1+y^2)^(1/2)+1/(1+(x-y)^2)^(1/2)" | valence | 1
%
%Coordinates
"helium"| 0 | 0
%
For more information on how to write a potential formula expression, see Input file.
We named the species “helium” instead of “He” because “He” is already the name of a pseudopotential for the actual 3D helium atom.
Running
The calculation should converge within 14 iterations. As usual, the results are summarized in the static/info file, where you can find
...
**************************** Theory Level ****************************
Input: [TheoryLevel = independent_particles]
**********************************************************************
SCF converged in 19 iterations
Some of the states are not fully converged!
Eigenvalues [H]
#st Spin Eigenvalue Occupation
1 -- -2.238257 1.000000
Energy [H]:
Total = -2.23825730
Free = -2.23825730
-----------
Ion-ion = 0.00000000
Eigenvalues = -2.23825730
Hartree = 0.00000000
Int[n*v_xc] = 0.00000000
Exchange = 0.00000000
Correlation = 0.00000000
vanderWaals = 0.00000000
Delta XC = 0.00000000
Entropy = 1.38629436
-TS = -0.00000000
Photon ex. = 0.00000000
Kinetic = 0.28972534
External = -2.52798263
Non-local = 0.00000000
Int[n*v_E] = 0.00000000
Dipole: [b] [Debye]
= 7.96347E-09 2.02411E-08
= 5.29240E-09 1.34519E-08
Convergence:
abs_energy = 1.18571819E-13 ( 0.00000000E+00) [H]
rel_energy = 5.29750620E-14 ( 0.00000000E+00)
abs_dens = 4.73568290E-08 ( 0.00000000E+00)
rel_dens = 4.73568290E-08 ( 1.00000000E-06)
abs_evsum = 1.18571819E-13 ( 0.00000000E+00) [H]
rel_evsum = 5.29750620E-14 ( 0.00000000E+00)
As we are running with non-interacting electrons, the Hartree, exchange and correlation components of the energy are zero. Also the ion-ion term is zero, as we only have one “ion”.
Unoccupied States
Now you can do just the same thing we did for the harmonic oscillator and change the unoccupied calculation mode:
CalculationMode = unocc
Dimensions = 2
TheoryLevel = independent_particles
BoxShape = parallelepiped
Lsize = 8
Spacing = 0.1
%Output
wfs | plane_z
%
OutputWfsNumber = "1-3"
%Species
"helium" | species_user_defined | potential_formula | "-2/(1+x^2)^(1/2)-2/(1+y^2)^(1/2)+1/(1+(x-y)^2)^(1/2)" | valence | 1
%
%Coordinates
"helium"| 0 | 0
%
ExtraStates = 5
We have added extra states and also restricted the wavefunctions to plot (OutputWfsNumber = "1-4,6").
The results of this calculation can be found in the file static/eigenvalues . In this case it looks like
Some of the states are not fully converged!
Criterion = 0.100000E-05
Eigenvalues [H]
#st Spin Eigenvalue Occupation Error
1 -- -2.238257 1.000000 (2.9E-06)
2 -- -1.815718 0.000000 (7.9E-07)
3 -- -1.701549 0.000000 (9.7E-07)
4 -- -1.629240 0.000000 (9.6E-07)
5 -- -1.608656 0.000000 (9.3E-07)
6 -- -1.509599 0.000000 (4.1E-07)
Apart from the eigenvalues and occupation numbers we asked Octopus to output the wave-functions. To plot them, we will use gnuplot. You start it and type
set xlabel "x1"
set ylabel "x2"
set t postscript enhanced color font "Monospace-Bold,20" landscape size 11,8.5
set key top left
set hidden3d
set pm3d
set contour
set ticslevel 0
unset key
unset surface
set output "Wfs-st0001.eps"
splot 'static/wf-st0001.z=0' using 1:2:3
set output "Wfs-st0002.eps"
splot 'static/wf-st0002.z=0' using 1:2:3
set output "Wfs-st0003.eps"
splot 'static/wf-st0003.z=0' using 1:2:3
We plot the ground-state, 1st and 2nd excited-state wave-functions. (If you get this, ignore it: warning: Cannot contour non grid data. Please use "set dgrid3d".) Which correspond to singlet and which to triplet states?
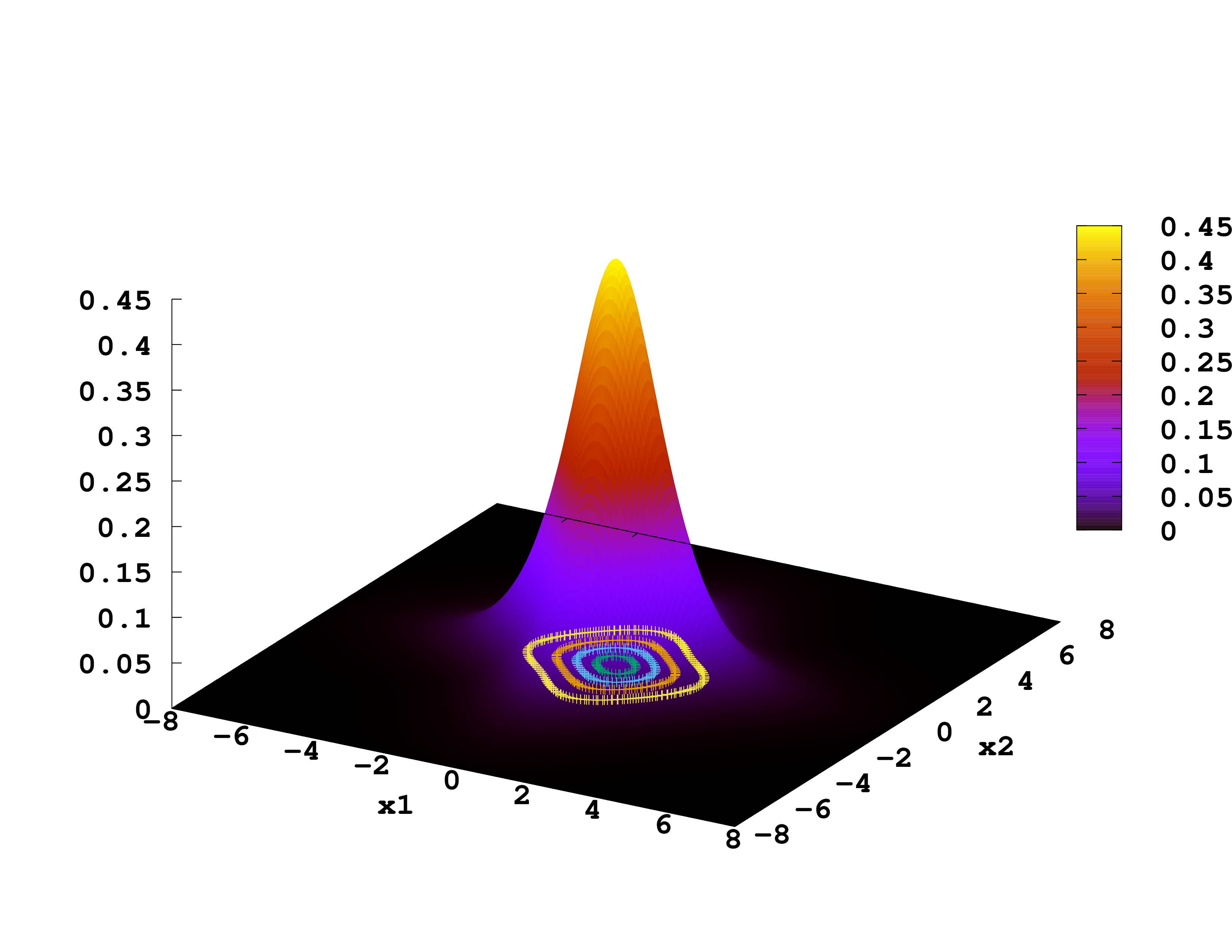
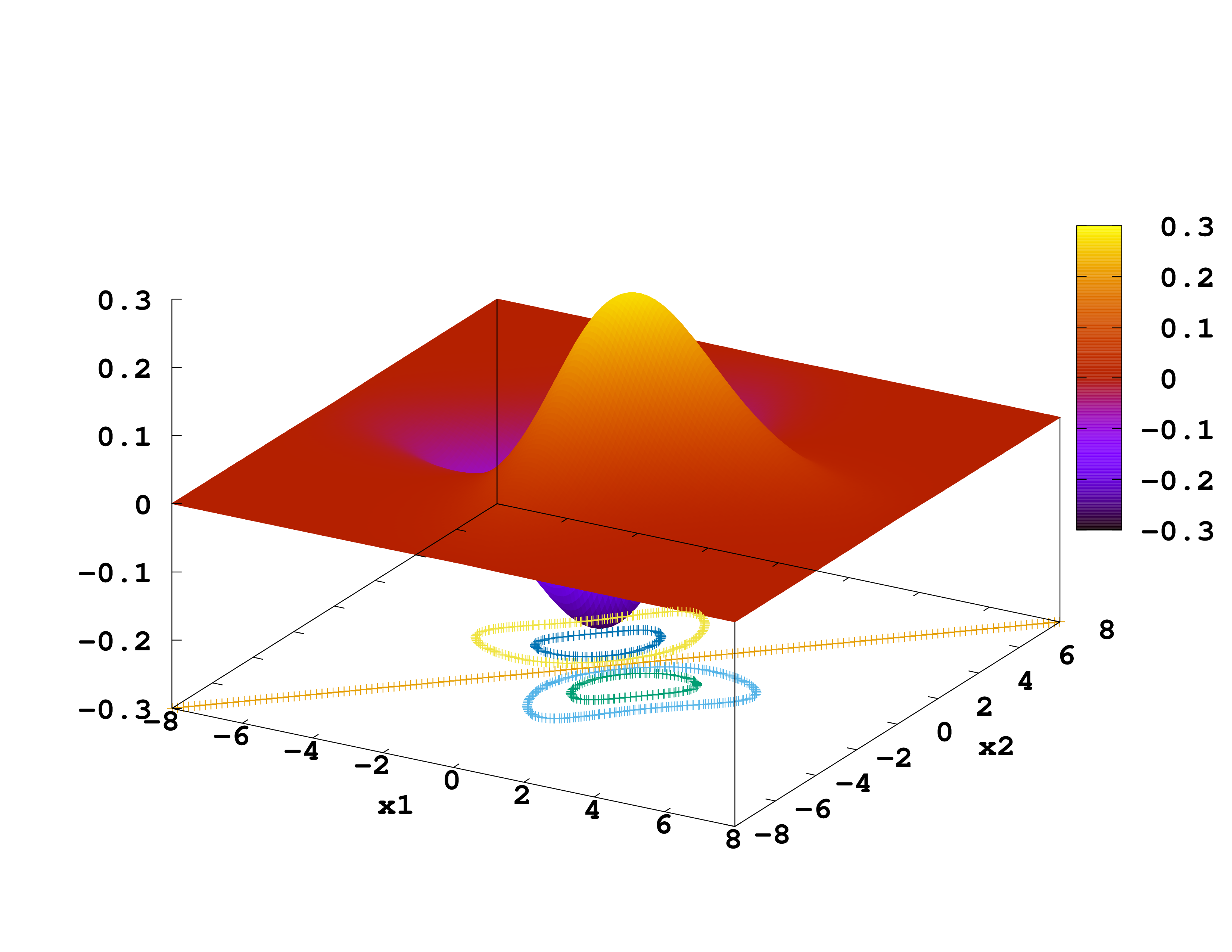
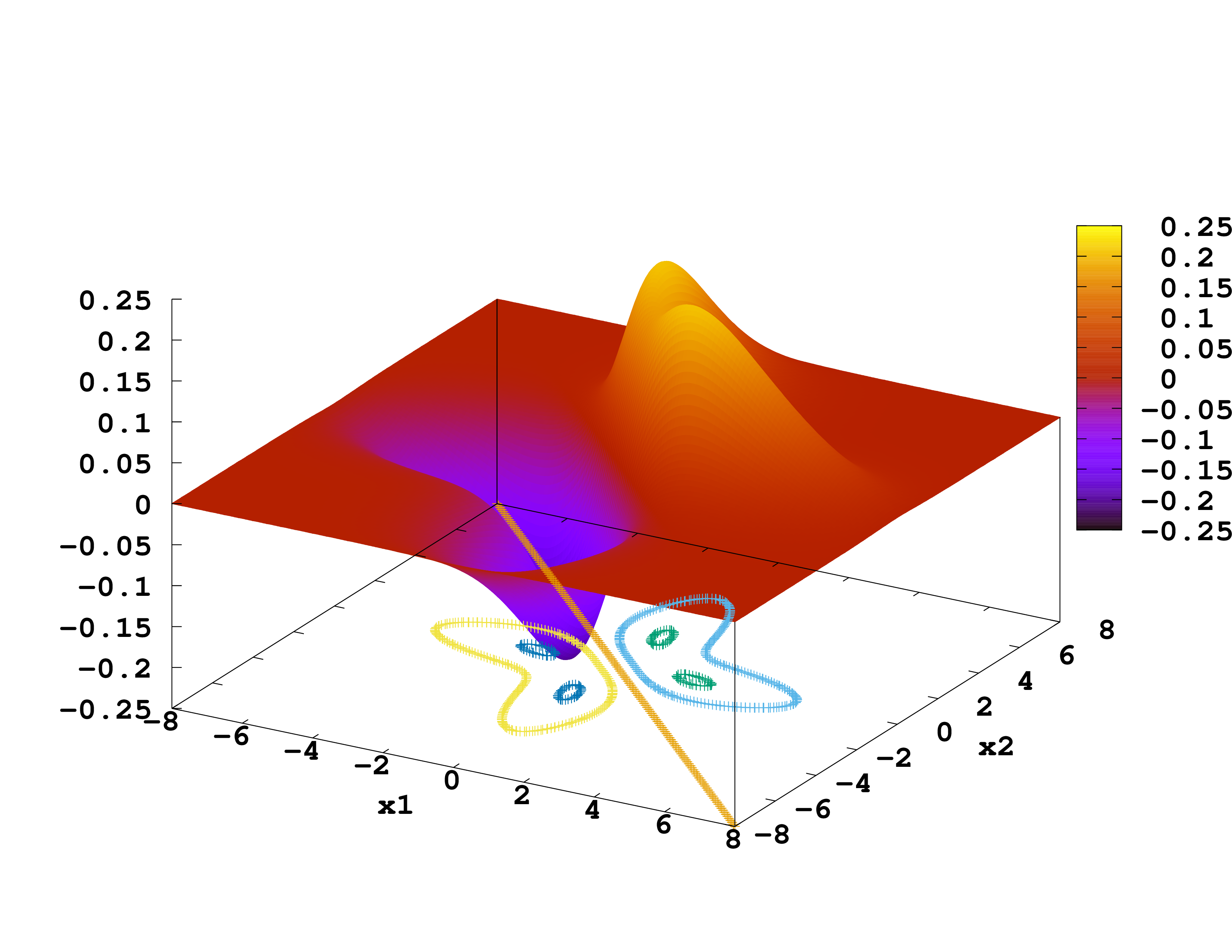
Exercises
-
Calculate the helium atom in 1D, assuming that the 2 electrons of helium do not interact (using Dimensions = 1). Can you justify the differences?
-
See how the results change when you change the interaction. Often one models the Coulomb interaction by $1/\sqrt{a^2+r^2},$, and fits the parameter $a,$ to reproduce some required property.