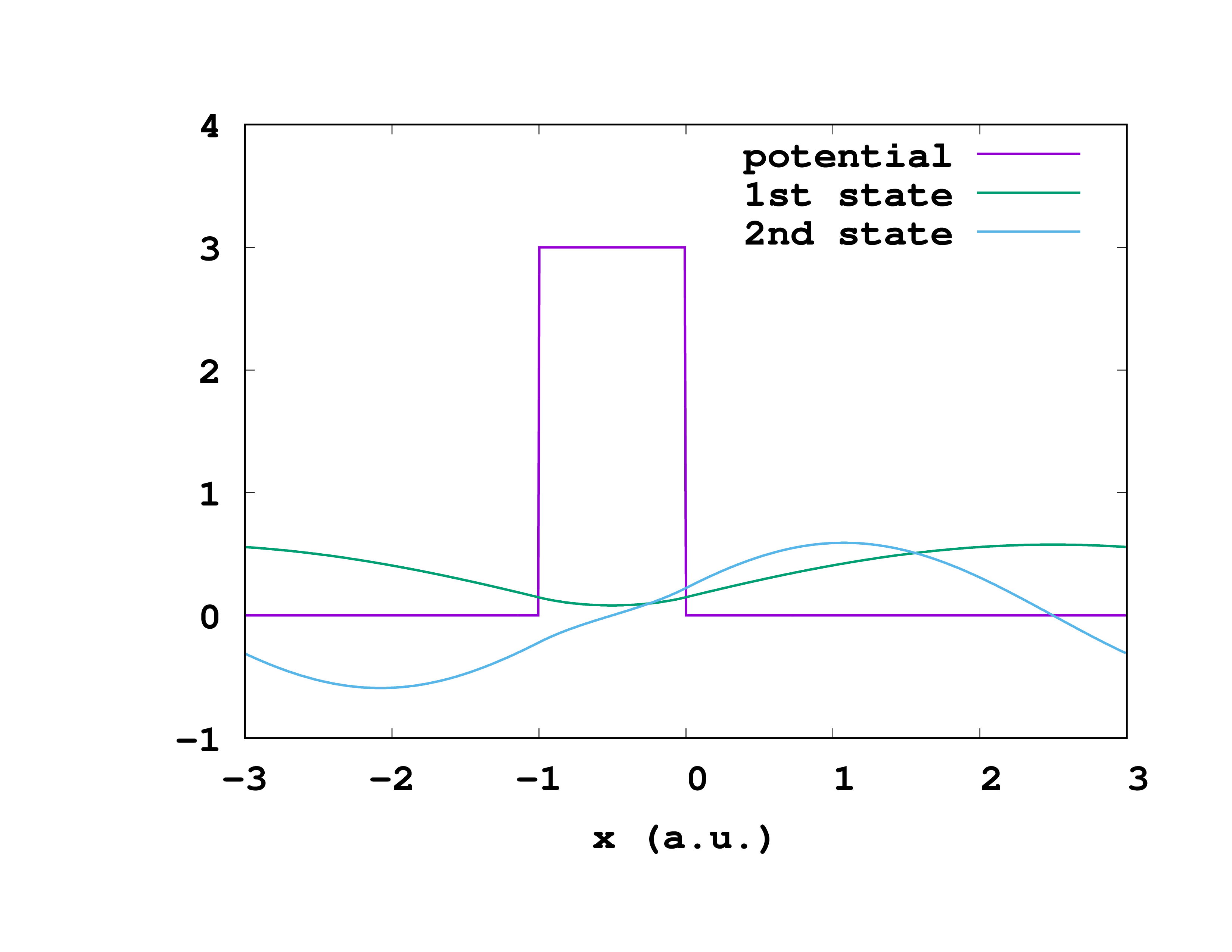
Kronig-Penney Model
The Kronig-Penney model is a 1D system that demonstrates band gaps, which relate to the allowed energies for electrons in a material. In this tutorial we calculate the bandstructure for Kronig-Penney Model. The Kronig-Penney Model has a periodic potential of
$$ V(x) = \begin{cases} V_0 & -b < x < 0 \cr 0 & 0 < x < a \end{cases} $$
Where b is the width of each barrier, and a is the spacing between them.
Input
The following input file will be used for the ground state calculation:
CalculationMode = gs
ExtraStates = 4
PeriodicDimensions = 1
Dimensions = 1
TheoryLevel = independent_particles
a = 5
b = 1
V = 3
Lsize = (a + b)/2
%LatticeParameters
a + b
%
Spacing = .0075
%Species
"A" | species_user_defined | potential_formula | "(x>-b)*V*(x<0)" | valence | 1
%
%Coordinates
"A" | 0 |
%
%KPointsGrid
11 |
%
%KPointsPath
11 |
0.0 |
0.5 |
%
ConvEigenError = true
%Output
potential
wfs
%
OutputFormat = axis_x
OutputWfsNumber = "1,2"
Bandstructure
To calculate the bandstructure simply change the CalculationMode to unocc.
CalculationMode = unocc
ExtraStates = 4
PeriodicDimensions = 1
Dimensions = 1
TheoryLevel = independent_particles
a = 5
b = 1
V = 3
Lsize = (a + b)/2
%LatticeParameters
a + b
%
Spacing = .0075
%Species
"A" | species_user_defined | potential_formula | "(x>-b)*V*(x<0)" | valence | 1
%
%Coordinates
"A" | 0 |
%
%KPointsGrid
11 |
%
%KPointsPath
11 |
0.0 |
0.5 |
%
ConvEigenError = true
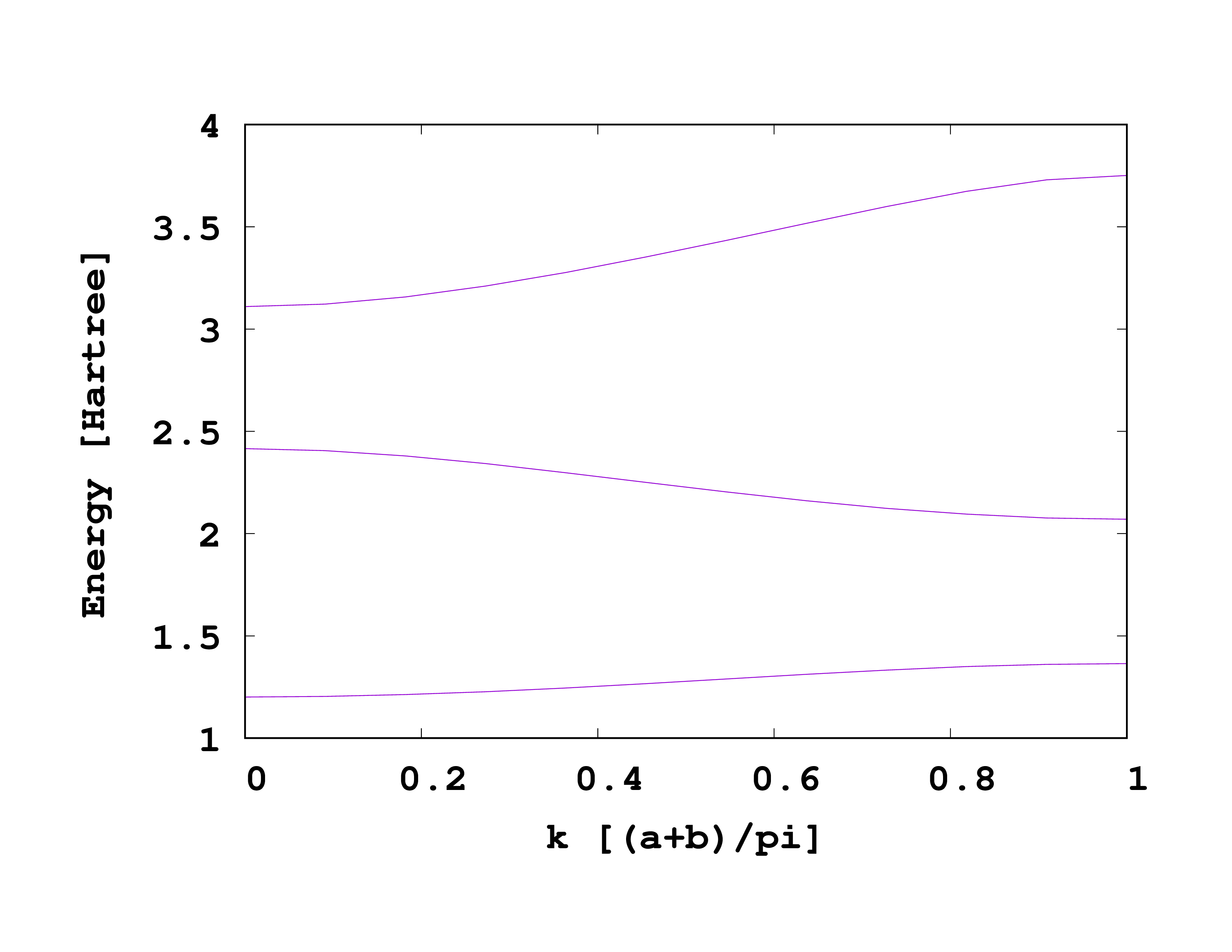
To plot the bandstructure, we will use the same command from the Periodic Systems (assuming you are using gnuplot).
set xlabel "k [(a+b)/pi]"
set ylabel "Energy [Hartree]"
set t postscript enhanced color font "Monospace-Bold,25" landscape size 11,8.5
set output "bandstructure.eps"
set key top left
set rmargin 4.5
set lmargin 10.5
set tmargin 3.2
set bmargin 5.5
plot for [col=5:5+9] 'static/bandstructure' u 1:(column(col)) w l notitle ls 1
Reference:
Sidebottom DL. Fundamentals of condensed matter and crystalline physics: an introduction for students of physics and materials science. New York: Cambridge University Press; 2012.