Plane waves in vacuum
Cosinoidal plane wave in vacuum
In this tutorial, we will describe the propagation of waves in vacuum. Let’s start with one wave with a cosinoidal envelope.
CalculationMode = td
ExperimentalFeatures = yes
%Systems
'Maxwell' | maxwell
%
lsize_mx = 12.0
dx_mx = 0.5
%Maxwell.Lsize
lsize_mx | lsize_mx | lsize_mx
%
%Maxwell.Spacing
dx_mx | dx_mx | dx_mx
%
%MaxwellBoundaryConditions
plane_waves | plane_waves | plane_waves
%
%MaxwellAbsorbingBoundaries
not_absorbing | not_absorbing | not_absorbing
%
TDSystemPropagator = exp_mid
timestep = 1 / ( sqrt(c^2/dx_mx^2 + c^2/dx_mx^2 + c^2/dx_mx^2) )
TDTimeStep = timestep
TDPropagationTime = 150*timestep
lambda1 = 10.0
omega1 = 2 * pi * c / lambda1
k1_x = omega1 / c
E1_z = 0.05
pw1 = 10.0
ps1_x = - 25.0
%MaxwellIncidentWaves
plane_wave_mx_function | 0 | 0 | E1_z | "plane_waves_function_1"
%
%MaxwellFunctions
"plane_waves_function_1" | mxf_cosinoidal_wave | k1_x | 0 | 0 | ps1_x | 0 | 0 | pw1
%
OutputFormat = plane_x + plane_y + plane_z + axis_x + axis_y + axis_z
%MaxwellOutput
electric_field
magnetic_field
maxwell_energy_density
%
MaxwellOutputInterval = 50
MaxwellTDOutput = maxwell_energy + maxwell_total_e_field + maxwell_total_b_field
The total size of the (physical) simulation box is 20.0 x 20.0 x 20.0 Bohr (10 Bohr half length in each direction) with a spacing of 0.5 Bohr in each direction. As discussed in the input overview, also the boundary points have to be accounted for when defining the box size in the input file. In other words, the user has to know how much space these points will add, which is given by the derivatives order (in this case, 4) times the spacing. This is 4 * 0.5 bohr = 2 bohr. Hence the total size of the simulation box is chosen to be 12.0 bohr in each direction.
lsize_mx = 12.0
dx_mx = 0.5
%Maxwell.Lsize
lsize_mx | lsize_mx | lsize_mx
%
%Maxwell.Spacing
dx_mx | dx_mx | dx_mx
%
The boundary conditions are chosen as plane waves to simulate the incoming wave without any absorption at the boundaries.
%MaxwellBoundaryConditions
plane_waves | plane_waves | plane_waves
%
%MaxwellAbsorbingBoundaries
not_absorbing | not_absorbing | not_absorbing
%
The simulation time step is set to the value given by the Courant condition.
For equal spacing in the three dimensions, this is equal to dt = spacing /
(sqrt(3)*c) = 0.002106 atomic units of time, in this case,
c being the speed of light in atomic units (137.03599).
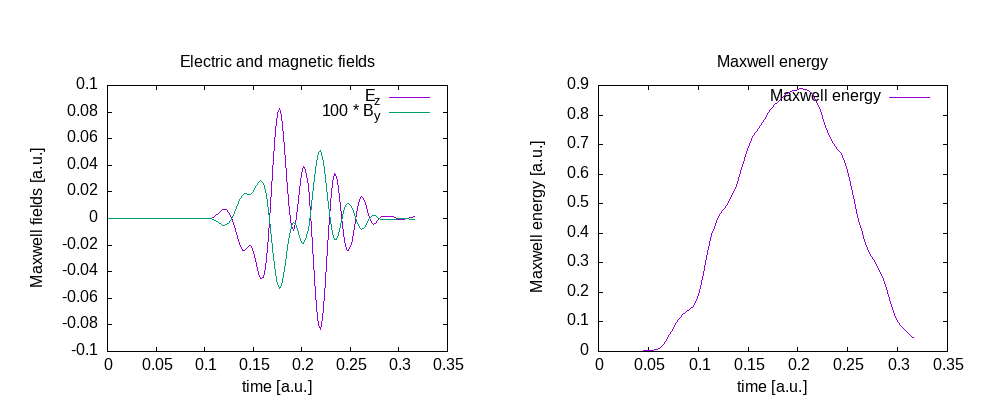
The system propagates 150 time steps = 0.316 atomic units.
TDSystemPropagator = exp_mid
timestep = 1 / ( sqrt(c^2/dx_mx^2 + c^2/dx_mx^2 + c^2/dx_mx^2) )
TDTimeStep = timestep
TDPropagationTime = 150*timestep
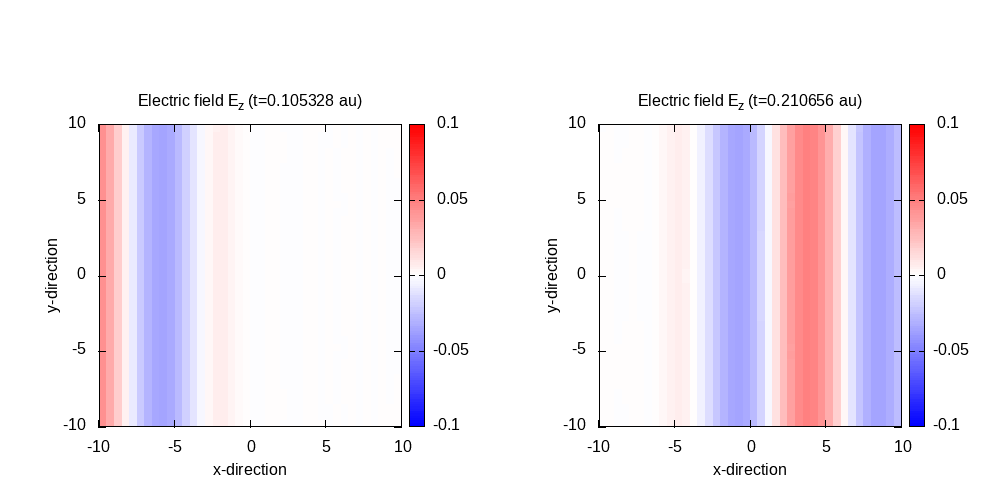
The incident cosinoidal plane is evaluated at the boundaries to be fed into the simulation box. The pulse has a width of 10.0 bohr, a spatial shift of 25.0 Bohr in the negative x-direction, an amplitude of 0.05 a.u., and a wavelength of 10.0 bohr.
lambda1 = 10.0
omega1 = 2 * pi * c / lambda1
k1_x = omega1 / c
E1_z = 0.05
pw1 = 10.0
ps1_x = - 25.0
%MaxwellIncidentWaves
plane_wave_mx_function | 0 | 0 | E1_z | "plane_waves_function_1"
%
%MaxwellFunctions
"plane_waves_function_1" | mxf_cosinoidal_wave | k1_x | 0 | 0 | ps1_x | 0 | 0 | pw1
%
Finally, the output options are set:
OutputFormat = plane_x + plane_y + plane_z + axis_x + axis_y + axis_z
%MaxwellOutput
electric_field
magnetic_field
maxwell_energy_density
%
MaxwellOutputInterval = 50
MaxwellTDOutput = maxwell_energy + maxwell_total_e_field + maxwell_total_b_field
Contour plot of the electric field in z-direction after 50 time steps (t=0.105) and 100 time steps (t=0.21):
Maxwell fields at the origin and Maxwell energy inside the free Maxwell propagation region of the simulation box:
Interference of two cosinoidal plane waves
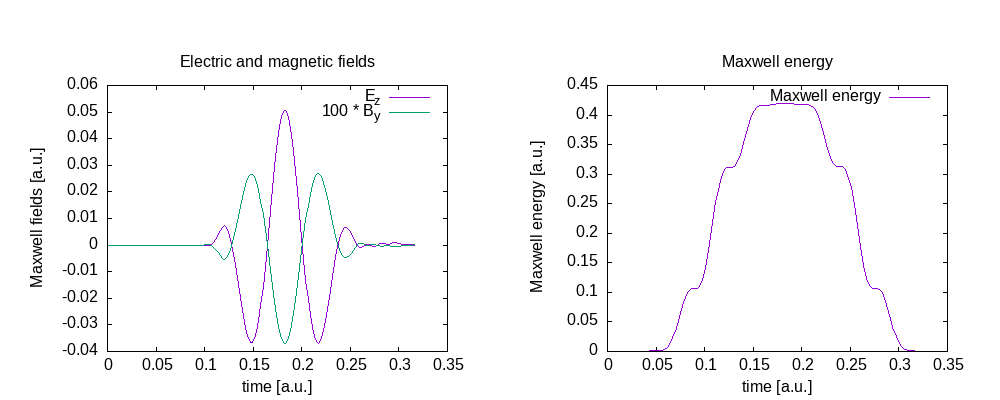
Instead of only one plane wave, we simulate in this example two different plane waves with different wave-vectors entering the simulation box, interfering and leaving the box again. In addition to the wave from the last tutorial, we add a second wave with different wave length, and entering the box at an angle, and shifted by 28 bohr along the corresponding direction of propagation. Both electric fields are polarized only in z-direction, and the magnetic field only in y-direction.
CalculationMode = td
ExperimentalFeatures = yes
%Systems
'Maxwell' | maxwell
%
lsize_mx = 12.0
dx_mx = 0.5
Maxwell.BoxShape = parallelepiped
%Maxwell.Lsize
lsize_mx | lsize_mx | lsize_mx
%
%Maxwell.Spacing
dx_mx | dx_mx | dx_mx
%
%MaxwellBoundaryConditions
plane_waves | plane_waves | plane_waves
%
%MaxwellAbsorbingBoundaries
not_absorbing | not_absorbing | not_absorbing
%
TDSystemPropagator = exp_mid
timestep = 1 / ( sqrt(c^2/dx_mx^2 + c^2/dx_mx^2 + c^2/dx_mx^2) )
TDTimeStep = timestep
TDPropagationTime = 150*timestep
OutputFormat = plane_x + plane_y + plane_z + axis_x + axis_y + axis_z
%MaxwellOutput
electric_field
magnetic_field
maxwell_energy_density
trans_electric_field
%
MaxwellOutputInterval = 50
MaxwellTDOutput = maxwell_energy + maxwell_total_e_field + maxwell_total_b_field
lambda1 = 10.0
omega1 = 2 * pi * c / lambda1
k1_x = omega1 / c
E1_z = 0.05
pw1 = 10.0
ps1_x = - 25.0
# second laser propagates in x-y direction
alpha = pi/4
lambda2 = 4.0
omega2 = 2 * pi * c / lambda2
k2_x = omega2 / c * cos(alpha)
k2_y = omega2 / c * sin(alpha)
E2_z = 0.05
pw2 = 10.0
ps2_x = - 28.0 * cos(alpha)
ps2_y = - 28.0 * sin(alpha)
%MaxwellIncidentWaves
plane_wave_mx_function | 0 | 0 | E1_z | "plane_waves_function_1"
plane_wave_mx_function | 0 | 0 | E2_z | "plane_waves_function_2"
%
%MaxwellFunctions
"plane_waves_function_1" | mxf_cosinoidal_wave | k1_x | 0 | 0 | ps1_x | 0 | 0 | pw1
"plane_waves_function_2" | mxf_cosinoidal_wave | k2_x | k2_y | 0 | ps2_x | ps2_y | 0 | pw2
%
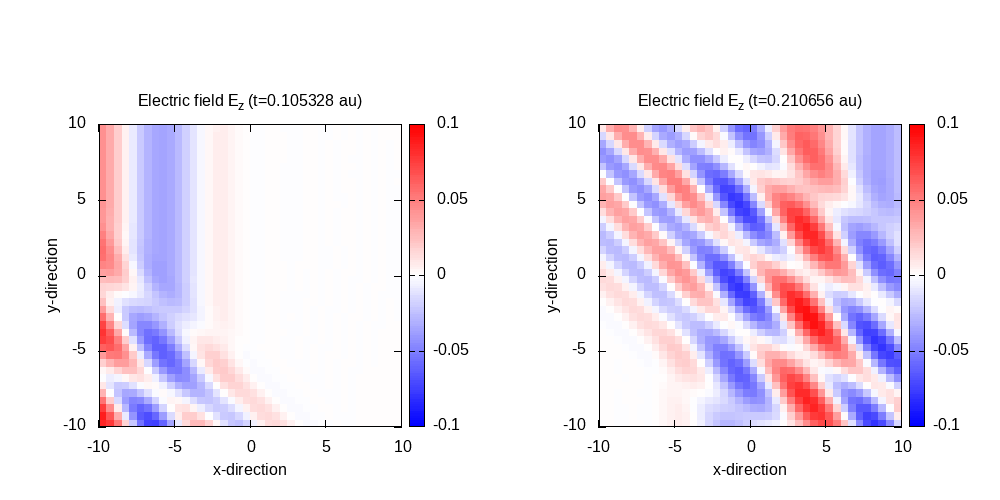
Using a similar scipt than in the previous example, the contour plots for the electric field in the z=0 plane can be obtained.
Contour plot of the electric field in z-direction after 50 time steps for
t=0.11 and 100 time steps for t=0.21:
Fields at the origin and total energy inside the propagation region of the simulation box: